“Seorang pemburu berjalan meninggalkan tendanya ke Selatan sejauh 10 km, lalu berbelok dan berjalan ke arah Timur sejauh 10 km. Pada titik ini ia melihat seekor beruang dan hendak menembaknya, tapi si beruang melawan dan dengan cakarnya ia mampu menjatuhkan senapan si pemburu. Si pemburu kabur terkencing-kencing ke Utara sejauh 10 km, dan ia menemukan kembali tendanya. Ia lalu ganti kolor dan istirahat. Apakah warna beruang tersebut?”
—Sebuah cerita lama dari buku teka-teki Matematika
PADA dua bagian sebelumnya kita telah mendiskusikan fenomena yang menjadi petunjuk bulatnya Bumi, bagaimana penganut Bumi datar menafsirkan fenomena yang sama, dan tidak konsistennya penafsiran ini dengan data yang ada.
Pada bagian ketiga ini, barangkali kita bisa mengakhiri serial tulisan ini dengan mendiskusikan satu aspek kebulatan Bumi yang juga penting: Hidup pada permukaan bola tidak sama dengan hidup pada bidang datar! Melengkungnya permukaan Bumi membawa konsekuensi-konsekuensi yang berbeda dengan realitas pada Bumi datar.
Bidang datar dan bidang melengkung

Apa beda bidang melengkung dengan bidang datar? Salah satunya adalah segitiga. Apabila kita menggambar segitiga di atas kertas, hitunglah jumlah total ketiga sudutnya, niscaya jumlahnya adalah 180°. Akan tetapi, bila kita menggambar segitiga pada permukaan melengkung, maka jumlah total ketiga sudut akan lebih dari 180° (Gambar 1).
Mengapa bisa demikian? Ini karena garis lurus pada permukaan bola bukanlah garis lurus pada bidang datar, dan begitu pula sebaliknya: garis lurus pada bidang datar bukanlah garis lurus pada permukaan bola. Untuk menggambar bidang datar macam segitiga, kita membutuhkan komponen-komponennya, yaitu garis lurus dan titik. Mari kita tinjau perbedaan keduanya pada bidang datar dan bidang melengkung.
Dalam geometri, titik adalah konsep primitif, artinya konsep yang tidak bisa lagi didefinisikan dengan konsep-konsep yang lebih mendasar1Jadi dalam konteks ini, primitif artinya bukan terbelakang atau bego seperti kalau kita menggunakan kata ini untuk mencela lawan bicara.. Garis lurus bukan lagi konsep primitif, karena dengan menggunakan dua titik kita bisa mendefinisikan sebuah garis lurus. Pun juga halnya dengan bangun datar, misalnya segitiga, karena dengan tiga titik dan garis lurus kita bisa mendefinisikan sebuah segitiga.

Garis lurus pada bidang datar adalah jarak terpendek antara dua titik, dan antara dua titik ini hanya ada satu garis lurus yang bisa digambar. Bagaimana kita mendefinisikan garis lurus pada permukaan bola? Marilah kita ambil satu titik pada permukaannya, lalu mari kita ikuti definisi garis lurus pada bidang datar: kita berjalan ke satu arah sembarang tanpa berbelok. Kali ini yang terjadi, sebagaimana kita ketahui, kita akan kembali ke titik semula (Gambar 2). Sekarang marilah kita memotong bola tersebut dengan mengikuti garis yang telah kita gambar (Gambar 3), dan kita akan melihat bahwa perpotongan mengikuti garis ini akan menghasilkan dua belahan bola yang berukuran dan berbentuk sama.

 Gambar 3. Apabila kita memotong bola sepanjang “garis lurus” yang telah kita gambar pada Gambar 2, kita akan melihat bahwa garis ini membelah bola menjadi belahan yang serupa. Foto dan ilustrasi oleh Tri L. Astraatmadja dan Ucu Agustin.
Gambar 3. Apabila kita memotong bola sepanjang “garis lurus” yang telah kita gambar pada Gambar 2, kita akan melihat bahwa garis ini membelah bola menjadi belahan yang serupa. Foto dan ilustrasi oleh Tri L. Astraatmadja dan Ucu Agustin.Dengan demikian inilah definisi garis lurus pada permukaan bola: Sebuah garis yang membelah bola tersebut menjadi dua bagian berukuran dan berbentuk serupa. Ada nama khusus untuk garis ini, yaitu lingkaran besar. Bila kita perhatikan, penampang silang perpotongan ini memang berbentuk lingkaran, dan lingkaran ini selalu berpusat pada titik pusat bola. Garis lurus antara titik A dan titik B pada permukaan bola, dengan demikian adalah sebuah busur dari lingkaran besar (Gambar 4), dan merupakan jarak terpendek antara A dan B.
Apabila istilah “garis lurus pada permukaan bola” membuat kita kurang sreg karena terlalu terbiasa dengan konsep garis lurus pada bidang datar, kita bisa menggunakan kata geodesik, yaitu generalisasi dari “garis lurus” pada permukaan melengkung.

Maka dengan menggunakan tiga segmen geodesik, kita dapat menggambar sebuah segitiga pada permukaan bola, seperti pada Gambar 1. Karena melengkungnya permukaan bola, maka kita bisa melihat bahwa jumlah ketiga sudut segitiga ini akan lebih dari 180°.
Karena kelengkungan inilah, sudut arah pada bidang melengkung akan berbeda dengan pada bidang datar. Navigasi pada permukaan melengkung, dengan demikian, akan berbeda dengan navigasi pada bidang datar. Salah satu contoh penggunaan geodesik untuk keperluan navigasi adalah pada penentuan rute penerbangan.
Geodesik dan arah pada permukaan melengkung
Apabila kita naik pesawat penerbangan jarak jauh, kita bisa melihat pada layar di kursi penumpang di depan kita, rute yang ditempuh dari bandara asal ke bandara tujuan. Hampir pasti garisnya akan melengkung, bukan? Contohnya misalnya pada panel kanan Gambar 5, ditunjukkan dengan garis merah adalah rute penerbangan dari Bandara Soekarno-Hatta ke Bandara Schiphol di Negeri Belanda. Nah garis melengkung warna merah ini sebenarnya adalah geodesik pada permukaan bola, yang diproyeksikan ke bidang datar. Karena geodesik adalah kurva terpendek antara dua titik pada permukaan melengkung, maka untuk mempercepat waktu penerbangan dan menghemat bahan bakar, rute pesawat antara kedua titik sebisa mungkin akan mengikuti geodesik2Saya katakan di sini sebisa mungkin, karena penentuan rute pesawat bukan hanya persoalan geometri, tetapi juga persoalan traktat antar bangsa, arah angin, dan situasi politik. Contoh terkini adalah penembakan pesawat Malaysia Airlines MH17 di langit Ukraina yang membuat rute-rute penerbangan internasional membelok menghindari langit Ukraina. Detail-detail mengenai kondisi-kondisi yang mempengaruhi penentuan rute penerbangan internasional dapat dibaca di artikel ini. Sebaliknya, garis lurus pada bidang datar, apabila diproyeksikan ke bidang melengkung, akan menjadi garis lengkung. Contoh adalah garis biru pada Gambar 5.
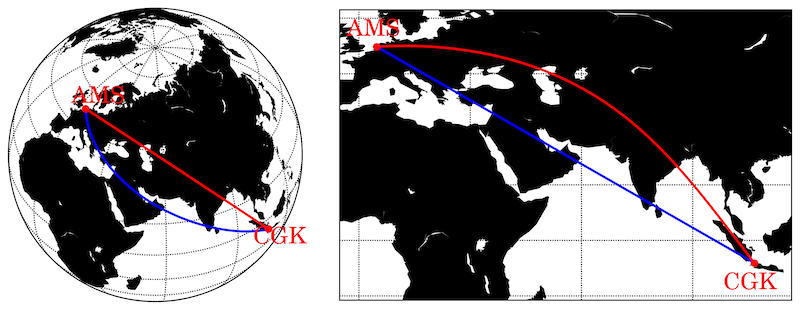
Apabila kita perhatikan lagi panel kanan Gambar 5, dan dengan mengingat bahwa garis merah adalah geodesik antara Cengkareng dan Schiphol, maka sesungguhnya arah terbang lurus menuju Schiphol dari Cengkareng adalah arah yang ditunjukkan oleh garis merah! Ini terdengar sukar dipercaya, karena secara intuitif kita akan berpikir bahwa arah terbang lurus menuju Schiphol adalah arah yang ditunjukkan oleh garis biru. Namun realitasnya, apabila kita terbang dari Cengkareng menuju Schiphol dengan mengikuti garis biru, maka kita harus terus menerus mengubah arah karena sejatinya garis tersebut bukanlah geodesik pada permukaan bola. Jadi: Dari Cengkareng ke Schiphol, terbanglah dalam arah azimuth 38° (diukur dari arah Utara ke Barat) sebagaimana ditunjukkan garis merah, bukan 60° seperti ditunjukkan garis biru.
Sebagaimana bisa kita lihat, perhitungan penentuan arah akan berbeda pada bidang datar dan pada permukaan bola. Untuk menentukan arah dan jarak antara dua titik pada bidang datar, kita cukup menggunakan geometri dan trigonometri yang diajarkan dari SD hingga SMA. Geometri ini adalah geometri yang berlaku pada bidang datar, disebut juga dengan Geometri Euklides. Pada permukaan bola, berlaku geometri yang lain lagi yaitu geometri bola, dan untuk menghitung arah dan jarak antara dua titik pada permukaan bola dibutuhkan trigonometri bola.
Barangkali dalam kehidupan sehari-hari kita gak butuh geometri bola, trigonometri bola, dan tetek-bengek lainnya. Bumi ini demikian besarnya sehingga ia tampak datar-datar saja dan untuk banyak keperluan, geometri bidang datar sudah cukup untuk menghitung luas sawah, lebar sungai, atau arah menuju warung. Untuk apa kita peduli perhitungan arah dan jarak pada permukaan bola?
Apabila Anda beragama dan saya boleh menebak agama Anda, saya punya peluang 87.2% tebakan saya benar bila saya menebak Anda beragama Islam3Peluang tebakan saya benar bisa ditingkatkan bila saya punya informasi tambahan soal Anda. TAPI INGAT! Judi (judiiiii) meracuni kehidupan! Hehehe…. Apabila Anda rajin sholat, maka saya kira Anda akan peduli paling tidak satu arah pada permukaan bola: Arah kiblat.
Kiblat dan penentuannya
Bagaimanakah arah kiblat ditentukan? Ya tentu saja dengan menggunakan trigonometri bola. Bila kita mengetahui koordinat (garis lintang dan garis bujur) dua titik pada permukaan bola, maka kita bisa menghitung dua hal: jarak antara kedua titik, dan sudut arah dari satu titik menuju titik yang lainnya. Di sekitar Tugu Monas di Jakarta, misalnya, dapat dihitung bahwa sudut arah kiblat adalah sekitar 64.85° diukur berlawanan arah jarum jam dari Utara ke arah Barat4Jika ada pembaca yang berminat bermatematika dan menghitung sendiri, saya dapat berikan formulanya, dengan memahami bahwa setiap persamaan matematika yang saya tulis akan mengurangi jumlah pembaca sebanyak 50%. Sebuah titik pada permukaan Bumi dapat dideskripsikan oleh koordinat garis lintang dan garis bujur (φ1, λ1). Sudut arah θ menuju titik lain pada permukaan Bumi, yang memiliki koordinat (φ2, λ2) adalah
\[\theta = \tan^{-1}\left[\frac{\sin(\lambda_1 – \lambda_2)}{\cos\phi_1\tan\phi_2 – \sin\phi_1\cos(\lambda_1-\lambda_2)}\right],\]
di mana sudut θ diukur berlawanan arah jarum jam dari arah Utara menuju arah Barat. Dengan memasukkan koordinat Ka’bah yaitu (φ2, λ2) = (21.4225, 39.8262), dan koordinat daerah sekitar Tugu Monas yaitu (misalnya) (φ1, λ1) = (-6.1745, 106.8227), maka dapat dihitung arah kiblat adalah θ = 64.85°. Hasil ini dapat dibandingkan situs-situs penyedia layanan pencarian arah kiblat, misalnya situs ini (harap perhatikan bahwa pada situs tersebut, arah kiblat diukur searah jarum jam dari arah Utara ke arah Timur).
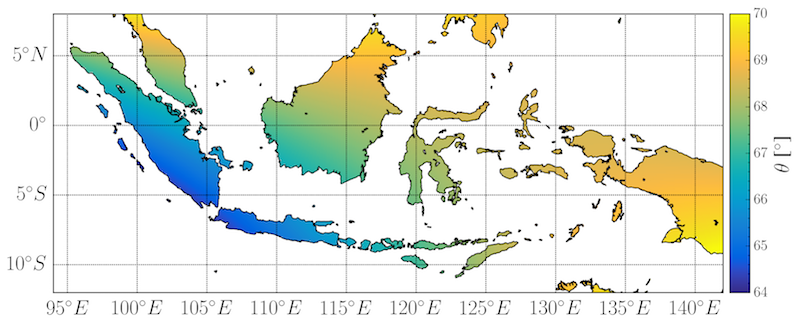
. Tentu saja arah kiblat akan berbeda dari tempat ke tempat, tapi untuk tempat-tempat yang jaraknya tak terlalu jauh, arah kiblat ini tidak akan jauh berbeda. Rumah orang tua saya yang jaraknya sekitar 12 km ke arah tenggara dari Tugu Monas, misalnya, bisa saja menggunakan arah kiblat yang diukur di Tugu Monas. Di tempat-tempat lain yang lebih jauh, tentunya sudut arah ini berbeda cukup jauh. Pada Gambar 6, dengan menggunakan trigonometri bola, saya menghitung sudut arah kiblat untuk seluruh titik daratan di wilayah Indonesia dan sekitarnya. Kita bisa lihat, untuk wilayah Indonesia dan sekitarnya, sudut arah kiblat berkisar antara 64° hingga 70°, atau bervariasi sekitar enam derajat.
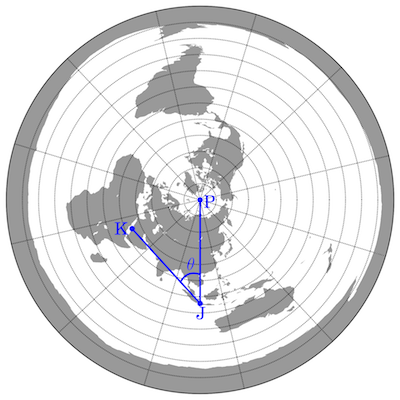
Apakah arah kiblat akan sama, apabila Bumi kita datar? Bila kita menggunakan koordinat yang sama dengan di atas untuk menghitung arah kiblat Bumi datar5Sekali lagi, jika ada pembaca yang berminat menghitung arah kiblat pada Bumi datar, berikut akan saya tuliskan formulanya (semoga 50% pembaca saya yang tersisa tidak mundur teratur). Pada Bumi datar, koordinat-kordinat geografis masih dapat digunakan, hanya saja dengan makna berbeda. Sudut arah θ menuju Ka’bah dari sebuah titik yang memiliki koordinat garis lintang dan garis bujur (φ, λ) pada Bumi datar adalah
\[\theta = \cos^{-1}\left[\frac{\left(\frac{\pi}{2}-\phi\right) – \left(\frac{\pi}{2}-\phi_K\right)\cos\left(\lambda_K – \lambda \right)}{\sqrt{\left(\frac{\pi}{2}-\phi\right)^2 + \left(\frac{\pi}{2}-\phi_K\right)^2 – 2\left(\frac{\pi}{2}-\phi\right)\left(\frac{\pi}{2}-\phi_K\right)\cos\left(\lambda_K – \lambda \right)}}\right],\] dengan (φK, λK) = (21.4225, 39.8262) adalah koordinat Ka’bah. Apabila kita memasukkan (φ, λ) = (-6.1745, 106.8227), maka dapat dihitung arah kiblat pada Bumi datar adalah θ = 42.30°. Ini berbeda sekali dengan arah kiblat pada permukaan bola. di Tugu Monas, maka kita akan memperoleh hasil 42.30° (Gambar 7). Angka ini jauh berbeda dengan 64.85° yang sebelumnya telah diperoleh dari perhitungan dengan menggunakan trigonometri bola.
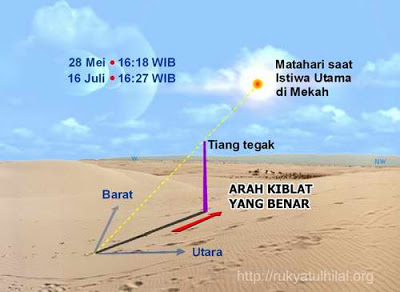
Dua kali dalam setahun, kita punya kesempatan untuk mengukur arah kiblat. Setiap akhir bulan Mei (tanggal 27 atau 28 Mei) dan pertengahan Juli (tanggal 15 atau 16 Juli), pada saat tengah hari di kota Mekkah, Matahari akan berada persis di zenith di atas Ka’bah. Nah pada saat itu terjadi, di manapun di muka Bumi ini apabila kita bisa melihat Matahari (dan tidak mendung), maka bayangan yang terbentuk akan menunjukkan arah kiblat (Gambar 8). Apabila kita berada di belahan Bumi yang tidak terkena sinar Matahari pada saat itu terjadi, maka jangan khawatir karena tentunya ada saat ketika Matahari persis berada di atas antipoda Ka’bah, yaitu pada tanggal 13 Januari dan 28 November. Antipoda adalah titik pada permukaan Bumi yang letaknya saling berseberangan, seolah-olah kedua titik ini adalah ujung-ujung sebuah galah yang melalui pusat Bumi. Contoh antipoda adalah Kutub Utara dan Kutub Selatan. Antipoda Jakarta dekat sekali dengan kota Bogotá di Colombia, sementara antipoda Ka’bah ada di tengah-tengah Samudera Pasifik, di dekat suatu atol di Polynesia Perancis.
Peristiwa hadirnya Matahari di zenith kota Mekkah ini terjadi karena bidang pergerakan semu Matahari di langit memiliki kemiringan 23.5° terhadap bidang khatulistiwa Bumi. Akibatnya, sepanjang tahun, posisi Matahari akan berkisar di antara 23.5° lintang selatan dan 23.5° lintang utara. Hanya di wilayah yang berada di antara kedua garis ini (dinamakan garis balik Selatan dan garis balik Utara), dua kali setahun Matahari akan berada di atas kepala pada saat tengah hari. Pada tanggal 20 Maret dan 22 September, misalnya, Matahari akan berada di atas khatulistiwa pada saat tengah hari. Ka’bah, karena berada pada lintang 21.42° Utara, juga mengalami hal ini setahun dua kali.
Bila pada pada bagian kedua saya mengajak Anda-Anda semua untuk mengukur keliling Bumi, kali ini saya akan mengajak Anda-Anda semua mengukur arah kiblat! Pada tahun 2017 ini, Matahari siang bolong akan berada di atas Ka’bah pada tanggal 27 Mei pukul 12:17:51 waktu setempat, atau pukul 16:17:51 WIB. Peristiwa ini akan terulang kembali pada tanggal 15 Juli, pada pukul 12:26:40 waktu setempat atau pukul 16:26:40 WIB. Siapkan perangkat sederhana untuk mengukur arah bayangan, dan Anda memiliki kesempatan untuk meluruskan arah kiblat. Tergantung pada lokasi Anda di Indonesia, sudut arah kiblat akan berkisar antara 64° hingga 70° (untuk persisnya berapa derajat di mana, lihat peta pada Gambar 6), hasil yang diperoleh dari trigonometri bola dan menjadi petunjuk tambahan bahwa Bumi ini bulat.
Metode yang amat sederhana, bisa dilakukan siapa saja, namun akurat ini telah digunakan oleh penduduk di daerah timur tengah semenjak jaman dahulu untuk mengoreksi arah kiblat. Di jaman modern ini, sudah banyak layanan internet yang dapat memberikan arah kiblat berdasarkan lokasi yang kita masukkan. Piranti lunak ini menghitungkan untuk kita arah kiblat dengan menggunakan formula trigonometri bola yang telah kita diskusikan sebelumnya. Tentu saja teknologi ini menawarkan kemudahan bagi kita, tapi tak ada salahnya kita kembali ke dasar dan mengetahui bagaimana perhitungan kiblat ini bekerja, dan bagaimana membuktikannya dengan menggunakan—lagi-lagi—tiang dan bayangan.
Epilog
Fanboys Bumi datar mencoba membuktikan pandangannya dengan mengambil asumsi yang tidak sesuai realitas (Matahari berada dekat sekali dan oleh karena itu sinarnya jatuh tak sejajar), dengan tidak mengacuhkan bukti-bukti yang tak sesuai dengan pandangan mereka (Misal: hanya mengukur jarak Matahari dengan menggunakan sepasang posisi, tapi tidak membandingkan hasilnya dengan pengukuran di tempat lain. Ini disebut juga dengan cherry-picking), dan juga dengan menjual agama. Penganut Bumi datar versi Kristen akan menjual penafsiran ayat-ayat Injil yang diklaim mendukung Bumi datar, sementara versi Islam akan menjual penafsiran mereka atas ayat-ayat Al-Qur’an. Karena orang Indonesia ada banyak dan hampir 90% masyarakat Indonesia beragama Islam, maka tak heran bila ada saja orang yang percaya ketika tafsir agama sudah dilibatkan. Persoalan penafsiran biarlah itu menjadi urusan orang lain yang lebih ahli, tapi dalam konteks ritual agama Islam yang paling mendasar, yaitu sholat lima waktu, kita telah memafhumi bahwa penentuan arah kiblat adalah salah satu hal penting, dan telah kita lihat bahwa seluruh perhitungan arah kiblat ini dilakukan dengan menggunakan formulasi yang dikembangkan untuk geometri bola. Terlebih lagi, angka-angka yang dihasilkan tokh bisa dibuktikan langsung pada tanggal 27 Mei dan 15 Juli setiap tahunnya, selama ribuan tahun semenjak orang sembahyang menghadap Ka’bah. Sesungguhnya setiap kali Anda sholat menghadap ke arah yang tepat, Anda dengan sendirinya telah membuktikan bahwa Bumi ini memang bulat.
Geometri bola dan trigonometri bola muncul di masa Yunani kuno sebagai pelengkap geometri Euklides, namun dikembangkan pada abad pertengahan oleh ilmuwan-ilmuwan muslim. Pengembangan geometri bola dimotivasi tidak hanya untuk keperluan pelayaran, tapi juga untuk keperluan ibadah: puasa dan sholat. Salah satu pionir subjek ini adalah al-Khwarizmi, ilmuwan Persia yang hidup pada abad 8–9 Masehi, di masa Kekhalifahan Abbasiyah. Nama Latin al-Khwarizmi, algorismus, kemudian menjadi asal kata algoritme. Kata aljabar, berasal dari metode yang ia ciptakan untuk menyelesaikan persamaan kuadrat. Ia juga adalah salah satu pengembang ilmu trigonometri bola, dan menurunkan formula untuk menghitung arah kiblat. Andai Al-Khwarizmi tiba-tiba hidup lagi dan mendengarkan para penganut Bumi datar menjual agama.. agama yang menjadi motivasinya untuk mengembangkan sebuah cabang ilmu pengetahuan yang kemudian tidak hanya membantunya memahami realitas dunia kita, tetapi juga memungkinkan orang bisa sholat sesuai dengan ketentuan… akan ngomong apakah beliau?
Masih banyak argumentasi penganut Bumi datar lainnya tapi tak perlu lah semua itu dijawab. Hal yang paling fundamental saya pikir telah kita diskusikan di sini, data mendasar telah kita buka dan bandingkan. Barangkali kita bisa tuntaskan tulisan ini sampai di sini saja. Akan tetapi, apabila ada hal-hal lain yang masih mengganjal, semoga rangkaian FAQ berikut ini bisa membantu.
Oh mudah-mudahan pada titik ini, teka-teki di awal artikel bisa terjawab. Beruang tersebut berwarna putih. Si pemburu berada di Kutub Utara.
Catatan kaki[+]
| ↑1 | Jadi dalam konteks ini, primitif artinya bukan terbelakang atau bego seperti kalau kita menggunakan kata ini untuk mencela lawan bicara. |
|---|---|
| ↑2 | Saya katakan di sini sebisa mungkin, karena penentuan rute pesawat bukan hanya persoalan geometri, tetapi juga persoalan traktat antar bangsa, arah angin, dan situasi politik. Contoh terkini adalah penembakan pesawat Malaysia Airlines MH17 di langit Ukraina yang membuat rute-rute penerbangan internasional membelok menghindari langit Ukraina. Detail-detail mengenai kondisi-kondisi yang mempengaruhi penentuan rute penerbangan internasional dapat dibaca di artikel ini |
| ↑3 | Peluang tebakan saya benar bisa ditingkatkan bila saya punya informasi tambahan soal Anda. TAPI INGAT! Judi (judiiiii) meracuni kehidupan! Hehehe… |
| ↑4 | Jika ada pembaca yang berminat bermatematika dan menghitung sendiri, saya dapat berikan formulanya, dengan memahami bahwa setiap persamaan matematika yang saya tulis akan mengurangi jumlah pembaca sebanyak 50%. Sebuah titik pada permukaan Bumi dapat dideskripsikan oleh koordinat garis lintang dan garis bujur (φ1, λ1). Sudut arah θ menuju titik lain pada permukaan Bumi, yang memiliki koordinat (φ2, λ2) adalah \[\theta = \tan^{-1}\left[\frac{\sin(\lambda_1 – \lambda_2)}{\cos\phi_1\tan\phi_2 – \sin\phi_1\cos(\lambda_1-\lambda_2)}\right],\] di mana sudut θ diukur berlawanan arah jarum jam dari arah Utara menuju arah Barat. Dengan memasukkan koordinat Ka’bah yaitu (φ2, λ2) = (21.4225, 39.8262), dan koordinat daerah sekitar Tugu Monas yaitu (misalnya) (φ1, λ1) = (-6.1745, 106.8227), maka dapat dihitung arah kiblat adalah θ = 64.85°. Hasil ini dapat dibandingkan situs-situs penyedia layanan pencarian arah kiblat, misalnya situs ini (harap perhatikan bahwa pada situs tersebut, arah kiblat diukur searah jarum jam dari arah Utara ke arah Timur). |
| ↑5 | Sekali lagi, jika ada pembaca yang berminat menghitung arah kiblat pada Bumi datar, berikut akan saya tuliskan formulanya (semoga 50% pembaca saya yang tersisa tidak mundur teratur). Pada Bumi datar, koordinat-kordinat geografis masih dapat digunakan, hanya saja dengan makna berbeda. Sudut arah θ menuju Ka’bah dari sebuah titik yang memiliki koordinat garis lintang dan garis bujur (φ, λ) pada Bumi datar adalah \[\theta = \cos^{-1}\left[\frac{\left(\frac{\pi}{2}-\phi\right) – \left(\frac{\pi}{2}-\phi_K\right)\cos\left(\lambda_K – \lambda \right)}{\sqrt{\left(\frac{\pi}{2}-\phi\right)^2 + \left(\frac{\pi}{2}-\phi_K\right)^2 – 2\left(\frac{\pi}{2}-\phi\right)\left(\frac{\pi}{2}-\phi_K\right)\cos\left(\lambda_K – \lambda \right)}}\right],\] dengan (φK, λK) = (21.4225, 39.8262) adalah koordinat Ka’bah. Apabila kita memasukkan (φ, λ) = (-6.1745, 106.8227), maka dapat dihitung arah kiblat pada Bumi datar adalah θ = 42.30°. Ini berbeda sekali dengan arah kiblat pada permukaan bola. |






